Théorie du gradient de traceur

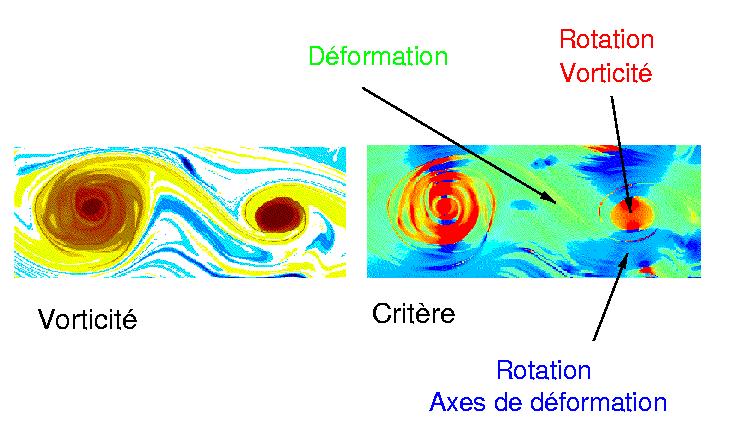
Evolution dans le temps d'une tache de traceur (en contour rouge) dans différents champs: à gauche, champ de déformation. Au milieu, champ de rotation pure (due à la vorticité relative). A droite, dans le champ de tourbillon circulaire.

• Premier cas. Dans un champ de déforlation pure (figure à gauche), on peut s'attendre à ca que la tache de traceur soit compressée le long de l'axe compressionnel de déformation et qu'elle soit étirée le long de l'axe extensionnel. En conséquence, le vecteur du gradient de traceur va s'aligner le long de l'axe compressionnel de déformation et la norme du gradient va croître exponteniellement dans le temps.
• Second cas. Dans un champ de rotation pure due à la vorticité (figure du milieu), le vecteur va tourner dans le temps alors que la norme ne va pas s'amplifier et rester autour de sa valeur initiale.
• On peut distinguer une troisième possibilité qui n'a pas été mise en évidence par les études antérieures sur le sujet dans le cas d'un tourbillon circulaire pour lequel la vorticité est concentré au coeur (tel que le vortex ponctuel). Le gradient de traceur est en rotation et la norme croît simplement linéairement dans le temps. Dans ce cas, la vorticité n'est pas responsable de la rotation. Donc il y a un autre mécanisme à prendre en compte. Si on examine l'évolution des axes de déformation, on voit clairement que c'est la rotation des axes de déformation qui est responsable de la rotation du gradient de traceur (voir Lapeyre et al 1999).

• l'effet de la déformation qui tend à aligner le gradient dans la direction de l'axe compression de déformation,
• l'effet de la rotation effective (due à la vorticité et aux axes de déformation) qui tend à faire tourner le gradient.

Une tache de traceur dans un champ composé à la fois de vorticité et de déformation. L'effet de la déformation est matérializé par les flèches rouges alors que l'effet de la rotation effective est en bleu. La figure à gauche montre le cas de l'équilibre entre les deux effets alors que la figure de droite montre le cas pour lequel le gradient de traceur change son orientation.

• Quand les processus de déformation dominent la rotation, il y a une orientation d'équilibre entre la déformation et la rotation. En plus, on peut montrer que le gradient de traceur va tendre vers cette orientation. Celle-ci est différente de l'axe compressionnel de déformation.
• Quand la rotation domine,le gradient va être en rotation à un taux qui varie au cours du temps. On peut montrer que statistiquement, il y aura une orientation préférentielle.

A gauche, différentes régions du champ turbulent avec les propriétés du gradient de traceur. A droite, loi de probabilité jointe entre le rapport déformation sur rotation effective et l'angle du gradient de traceur avec l'axe compressionnel de déformation. La courbe noire est la loi théorique qui est bien vérifiée.